こんばんは。
今日はクラス分類に用いることができる線形モデルを紹介します。
(ロジスティック回帰がメインです)
それぞれの線形モデルの境界線を表示してみる
今回使用するデータはmglearnに含まれるforgeデータと、sklearnに含まれるcancerデータです。
まずは、forgeデータの可視化と、ロジスティック回帰と線形サポートベクタマシンによる分類を行ってみます。
# ライブラリのインポート from sklearn.linear_model import LogisticRegression # ロジスティック回帰 from sklearn.svm import LinearSVC # SVM import numpy as np import matplotlib.pyplot as plt import pandas as pd import mglearn from IPython.display import display %matplotlib inline # データの読み込み X, y = mglearn.datasets.make_forge() X.shape, y.shape # => ((26, 2), (26,)) fig, axes = plt.subplots(1, 2, figsize=(10, 3)) # SVC, ロジスティック回帰のモデルを定義し、それぞれプロット for model, ax, in zip([LinearSVC(), LogisticRegression()], axes): clf = model.fit(X, y) mglearn.plots.plot_2d_separator(clf, X, fill=False, eps=0.5, ax=ax, alpha=0.7) mglearn.discrete_scatter(X[:,0], X[:,1], y, ax=ax) ax.set_title("{}".format(clf.__class__.__name__)) ax.set_xlabel("Feature 0") ax.set_ylabel("Feature 1") axes[0].legend()
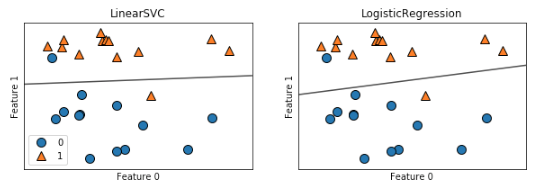
上記のように境界線が引かれ、2クラス分類が実行されます。
平行に近い直線で分類されていることが分かりますね。
では、この直線をもう少しデータに寄せる形に変更したい場合について、
正則化を決定するパラメータCの値を変更して学習させてみましょう。
正則化パラメータ:Cの変更
パラメータCとは正則化の強度を決定するパラメータのことで、デフォルトでは1が設定されます。
このCを大きくすると正則化が弱くなり、小さくすると、正則化が強くなります。
mglearn.plots.plot_linear_svc_regularization()
こんな感じ
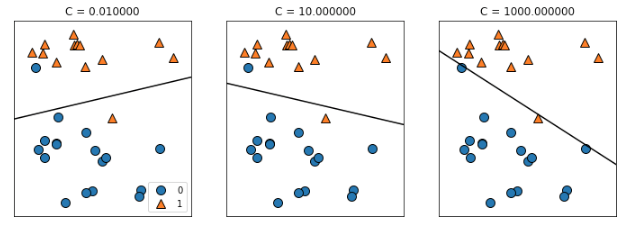
上図からも分かるように、Cの値が小さい時は正則化が強くなりすぎており、クラス分類に失敗していますよね。
逆にCの値が大きい時、クラス0の全ての点を正しく分類できていることが分かります。
(このデータセットは、全てのデータを直線で分類できないため、クラス1の一部データは正しく分類できません)
この一番右のモデルは、全ての点を正しくクラス分類することに注力するあまり、クラス全体としてのレイアウトを捉えきれてない可能性が高いです。
つまり、このモデルは過剰適合(過学習)してしまっていると推測できます。
ここまで見てきて、線形モデルによるクラス分類は、低次元空間においては制約が強すぎてあまり適していないと考えるのが妥当だと感じる人が多いと思います。
(実際に自分もそう感じました)
しかし、高次元の場合には線形モデルによるクラス分類は非常に強力になるため、特徴量の数が多い場合には過剰適合(過学習)を回避する方法を検討することが重要となるようです。
次のセクションで、ロジスティック回帰とcancerデータセット(特徴量の多いデータセット)を用いて、詳しく解析してみます。
ロジスティック回帰とcancerデータセット
ここでは、cancerデータセットを用いて、正則化パラメータ:Cの値を0.01, 1, 100と変化させた時の係数の変化を確認してみましょう。
from sklearn.datasets import load_breast_cancer from sklearn.model_selection import train_test_split cancer = load_breast_cancer() # データの分割 X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=42) # モデルの定義 # LogisticRegressionはデフォルトでL2正則化が行われる logreg = LogisticRegression().fit(X_train, y_train) print("Training set score: {:0.3f}".format(logreg.score(X_train, y_train))) print("Test set score: {:0.3f}".format(logreg.score(X_test, y_test))) # => Training set score: 0.955 # => Test set score: 0.958 # Cの値を変更してみる # 100 logreg100 = LogisticRegression(C=100).fit(X_train, y_train) print("Training set score: {:0.3f}".format(logreg100.score(X_train, y_train))) print("Test set score: {:0.3f}".format(logreg100.score(X_test, y_test))) # =>Training set score: 0.974 # =>Test set score: 0.965 # C次に = 0.01とし、正規化を強力にしてみる logreg001 = LogisticRegression(C=0.01).fit(X_train, y_train) print("Training set score: {:0.3f}".format(logreg001.score(X_train, y_train))) print("Test set score: {:0.3f}".format(logreg001.score(X_test, y_test))) # =>Training set score: 0.934 # =>Test set score: 0.930
上の結果から、C=100に設定すると、C=1のときと比べて訓練セット、テストセット共に精度が向上していることが分かります。
また、C=0.01とし、正則化を強力にした場合、適合不足に陥っているという推測も行うことができます。
ここで、上記3つのCに対して、学習された係数(重み)を描画してみましょう。
plt.plot(logreg.coef_.T, 'o', label='C=1') plt.plot(logreg100.coef_.T, '^', label='C=100') plt.plot(logreg001.coef_.T, 'v', label='C=0.01') plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90) plt.hlines(0, 0, cancer.data.shape[1]) plt.ylim(-5, 5) plt.xlabel('Feature') plt.ylabel('Coefficient magnitude') plt.legend()
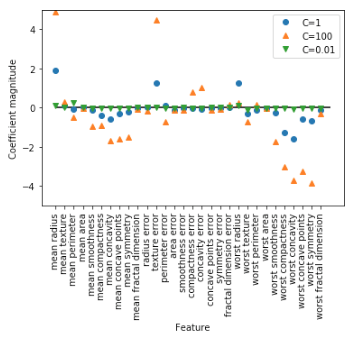
L2正則化を強力にする(Cの値を小さくする)と、係数(パラメータ)の値が0近くに押し込まれていることが分かります。
上記の場合、係数の絶対値が大きい特徴量に関してはクラス分類に大きな影響を与えているということが考えられますよね。
また、L1正規化を使用すると、よりモデルが解釈しやすくなります。
こちらも可視化してみましょう。
for C, marker in zip([0.01, 1, 100], ['v', 'o', '^']): lr_l1 = LogisticRegression(C=C, penalty='l1').fit(X_train, y_train) print("Training accuracy of L1 logreg with C = {:0.3f}: {:0.2f}".format(C, lr_l1.score(X_train, y_train))) print("Test accuracy of L1logreg with C = {:0.3f}: {:0.2f}".format(C, lr_l1.score(X_test, y_test))) plt.plot(lr_l1.coef_.T, marker, label = "C={:0.3f}".format(C)) plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90) plt.hlines(0, 0, cancer.data.shape[1]) plt.ylim(-5, 5) plt.xlabel('Feature') plt.ylabel('Coefficient magnitude') plt.legend(loc=3) # =>Training accuracy of L1 logreg with C = 0.010: 0.92 # =>Test accuracy of L1logreg with C = 0.010: 0.93 # =>Training accuracy of L1 logreg with C = 1.000: 0.96 # =>Test accuracy of L1logreg with C = 1.000: 0.96 # =>Training accuracy of L1 logreg with C = 100.000: 0.99 # =>Test accuracy of L1logreg with C = 100.000: 0.98
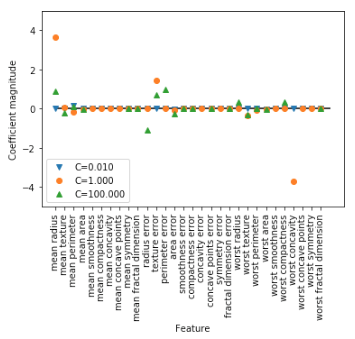
このように、L1正則化を行うことにより、どの特徴量がクラス分類に影響を与えているかが、L2正則化より鮮明に理解することができるようになります。
今日の勉強はここで終わり。
p.s. 第100回 甲子園大会始まりましたね!
甲子園球児をみてたら、今のチームでもっと活躍したいという衝動に駆られ、
(実は2つの草野球チームに所属している)
新宿の野球用品店に行き、木製バットを購入してきました。
(一人で練習するといったらやっぱり素振りですよね...あんまり好きじゃないけど。笑)
そして、涼しくなってきた21時頃に「よし素振りするか」と思って隣の公園に行きました。
...
...
5分で5箇所も蚊にさされました
(もちろん素振りは断念しました)
明日の仕事終わりに虫除けスプレー買ってきます。